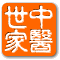
在消除动力学模型中已介绍,当体内药量(血药浓度)超过机体最大消除能力时,将为恒量消除的零级动力学,而药量(血药浓度)降至最大消除能力以下,将转化为恒比消除的一级动力学(图9-11)。这种存在动力学转换的情况下,药物的消除不能用一种统一简单的线性过程描述,故称非线性动力学(nonlinearpharmacokinetics)消除。若某药使用的剂量能使其在体内的消除由一级动力学转为零级,继续使用该剂量,血药浓度将会出现持续上升,而不能达到稳态浓度。对于安全范围狭窄的药物出现这种情况,是十分危险的。在需进行TDM的药物中,苯妥英钠、氨茶碱等在常用治疗剂量下就存在这种情况。
造成这种药动学方式转化的原因,主要是体内药量(血药浓度)超过了机体生物转化酶系的最大催化能力,即出现了饱和代谢,故亦常用描述酶促反应动力学的米氏方程表达非线性动力学消除的速率,即

式中Vm为最大消除速率,Km为米氏常数,相当于恰可产生Vm/2时的药物浓度。当C<<Km时,式(26)可变为
dc/dt=VmKm,令0k=Vmdc/kmdt,则dc/dt=-kC
此即前面已介绍的典型一级消除动力学微分表达式。而当C>>Km时,式(26)可写作
dC/dt=-Vm
上式为典型的零级消除动力学微分表达式。
由式(26)可推导得非线性动力学消除时的有关药动学参数计算公式:


图9-11 非线性动力学消除血药浓度-时间关系示意图
从上述各式中可看出,非线性消除动力学药物的多数参数均为随药物浓度而变化的变量,并非常数。在非线性动力学消除的药物TDM工作中,Vm和Km是两个十分有用的基本常数。必须注意的是,在药物体内过程中,生物转化能力影响因素多,个体差异尤为显著,因此Vm和Km个体差异大。在应用这两个参数的群体均值制定的剂量方案,往往不能达到预期效果。对于需长期用药或完全范围窄的药物,按下面方法确定具体个体的Vm和Km值实属必要。
不同时点取血测定血药浓度,依次求得相邻时点血药浓度及时间差值△C和△t。将式(26)中的dC/dt视做△C/△t,即消除速率V,而以相应两时点血药浓度均值C作为产生相应速率改变的浓度,分别代入式(26),并取倒数整理得:

式(27)为1/V随1/C变化的直线方程(图9-12)。该直线与纵轴交点为1/Vm,斜率为Vm/Km,故可分别求出Vm和Km。

图9-12 双倒数法求算非线性动力学消除的Vm和Km示意图
根据非线性动力学消除的特点,多剂用药时,只有当药物进入体内的速率R(量/d)恰与药物自体内的消除速率相等时,才有可能达稳态浓度Css。借用式(26)可得
R=Vm·Cm/Km+Cm式(28)
由此可得Css=Km·R/Vm-R式(29)
由上两式可计算出非线性动力学消除的药物,欲达某稳态浓度所需的用药速率(每日用药量),或按某速率用药时所能达到的稳态浓度,在这类药物的TDM工作中极为有用。从式(28)、(29)中也可看出,Vm和Km是必须首先求算出的基础。